Temperamento igual

El temperamento igual - de uso común en nuestros días - divide la octava en 12 semitonos de igual tamaño. Fue propuesto desde el siglo XVI:

• 1581: Vicenzo Galilei (1520-1591) sugiere dividir la octava en partes iguales usando la relación 18/17 para el semitono que aunque no es exacta se aproxima
• ca. 1580: el matemático holandés Simon Stevin (1548-1630) calcula el tamaño del semitono
• 1584: en China Zhu Zaiyu calcula la escala con precisión usando la razón 749:500 para la quinta

Sin embargo, no es hasta entrado el siglo XIX que comienza a usarse con la reticencia de algunos:

• 1906: Busoni estima que se trata de un mal de la civilización
• 1907: Saint-Saëns lo considera un tirano devastador y una herejía ... Reconoce sin embargo que ha sido demasiado fecundo para permitirnos deplorarlo

(citas de Musique et témperaments, Pierre-Yves Asselin)

El semitono igual

¿Cómo calculamos el tamaño del semitono que divide una octava en doce partes iguales? Si usamos la raíz cuadrada para dividir la tercera en dos tonos de igual tamaño, podemos entonces usar la raíz 12 de 2 (tamaño de la octava) para obtener el tamaño del semitono en el temperamento igual:

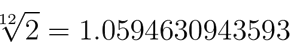
Podemos comprobar que partiendo de un do podemos llegar semitono a semitono hasta el do que se encuentra a una octava multiplicando por este número:

do	262
do#	277.6	262 x 1.0594630943593
re	294.1	277.6 x 1.0594630943593
re#	311.6	294.1 x 1.0594630943593
mi	330.1	311.6 x 1.0594630943593
fa	349.7	330.1 x 1.0594630943593
fa#	370.5	349.7 x 1.0594630943593
sol	392.6	370.5 x 1.0594630943593
sol#	415.9	392.6 x 1.0594630943593
la	440.6	415.9 x 1.0594630943593
la#	466.8	440.6 x 1.0594630943593
si	494.6	466.8 x 1.0594630943593
do	524	494.6 x 1.0594630943593

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivar 4.0 Internacional.
Publicado por teoria.com.