2,500 years of musical temperaments
A dialogue between human beings and nature
José Rodríguez Alvira
Equal Temperament
Equal temperament - the system in use today - divides the octave into 12 equal semitones. It has been proposed since the sixteenth century:
- 1581: Vincenzo Galilei (1520-1591) proposes dividing the octave into 12 equal parts, using the ratio 18/17 for the semitone.
- ca. 1580: Dutch mathematician Simon Stevin (1548-1630) calculates the size of the semitone.
- 1584: In China, Zhu Zaiyu accurately calculated the scale using the ratio of 749:500 for the fifth.
However, it was not until the nineteenth century that it began to be used, albeit reluctantly by some:
- 1906: Busoni considers that it is an evil of civilization
- 1907: Saint-Saëns considered it a devastating tyrant and heresy ... recognizes, however, that it has been too fruitful to be ignored
(from Musique et témperaments, Pierre-Yves Asselin)
The equal temperament semitone
How do we calculate the size of the semitone that divides an octave into twelve equal parts? If we were able to divide the third into two equal tones using the square root, then we can divide the octave into 12 equal parts by calculating the twelve root of 2 (octave):
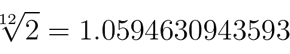
We can use this number to calculate the frequency of each semitone, as the following table shows:
| C | 262 | |
| C# | 277.6 | 262 x 1.0594630943593 |
| D | 294.1 | 277.6 x 1.0594630943593 |
| D# | 311.6 | 294.1 x 1.0594630943593 |
| E | 330.1 | 311.6 x 1.0594630943593 |
| F | 349.7 | 330.1 x 1.0594630943593 |
| F# | 370.5 | 349.7 x 1.0594630943593 |
| G | 392.6 | 370.5 x 1.0594630943593 |
| G# | 415.9 | 392.6 x 1.0594630943593 |
| A | 440.6 | 415.9 x 1.0594630943593 |
| A# | 466.8 | 440.6 x 1.0594630943593 |
| B | 494.6 | 466.8 x 1.0594630943593 |
| C | 524 | 494.6 x 1.0594630943593 |

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.