La serie armónica

Debemos comenzar por explicar un fenómeno acústico conocido como serie armónica. Cuando escuchamos un sonido producido por un instrumento musical estamos en realidad escuchando una multiplicidad de sonidos que forman la serie armónica.

Ya en el siglo XVII el francés Joseph Sauveur (1653-1716) y el inglés Thomas Pigot (1657-1686) notaron que las cuerdas al vibrar vibran por secciones, fenómeno que explica el por qué una sola cuerda produce esta multiplicidad de sonidos.

El vídeo a continuación muestra el análisis de espectro del do dos octavas por debajo del do central (C2). Cada uno de los picos representa un armónico de la serie:

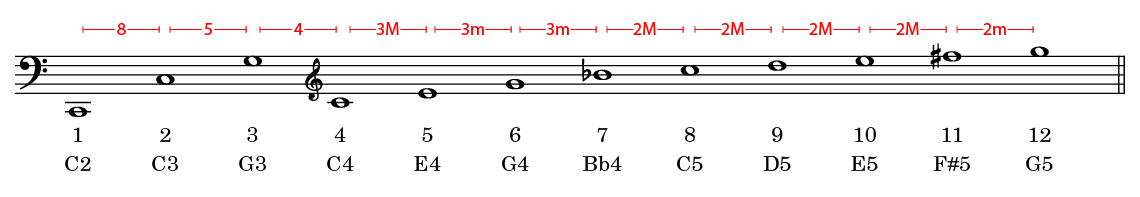
Algunos puntos a señalar:

• Hemos escrito las notas musicales correspondientes a los primeros 12 armónicos de la serie. Es obvio que son muchos los armónicos que siguen a estos primeros armónicos.
• El primer armónico o fundamental no es necesariamente el armónico más fuerte.
• El balance entre los armónicos varía constantemente. Esto, junto con la inmensa cantidad de armónicos explica la dificultad con que nos encontramos al sintetizar sonidos.

Importancia de la serie

El diálogo entre el ser humano y la naturaleza - al que hacemos referencia en el subtitulo de este artículo - gira en torno a la serie armónica. Podríamos decir que la naturaleza nos habla con la serie armónica y el ser humano responde con los diferentes sistemas de afinación que discutiremos.

La serie armónica define muchos de nuestros intervalos. A continuación señalamos la octava, quinta, cuarta, tercera mayor y séptima menor:

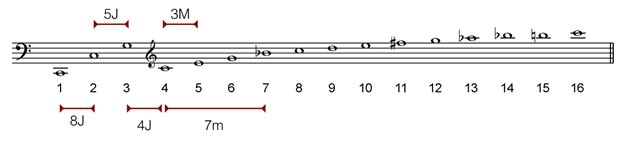
Podemos calcular la razón matemática (o tamaño) de los intervalos dividiendo la frecuencia de las notas. A continuación presentamos la frecuencia de algunos armónicos y calculamos en la tabla el tamaño de algunos intervalos:

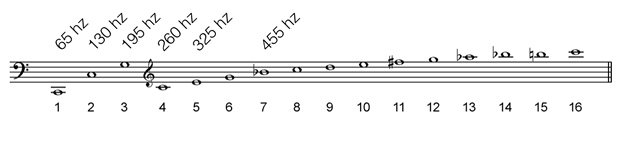
Intervalo	Razón	Se obtiene de las frecuencias de los armónicos
Octava	130 / 65 = 2	1 y 2
Quinta	195 / 130 = 1.5	2 y 3
Cuarta	260 / 195 = 1.33	3 y 4
Tercera mayor	325 / 260 = 1.25	4 y 5
Séptima menor	455 / 260 = 1.75	4 y 7

Curiosamente no necesitamos las frecuencias, podemos calcular los valores usando los números de los armónicos:

Intervalo	Razón	Armónicos
Octava	2 / 1 = 2	1 y 2
Quinta	3 / 2 = 1.5	2 y 3
Cuarta	4 / 3 = 1.33	3 y 4
Tercera mayor	5 / 4 = 1.25	4 y 5
Séptima menor	7 / 4 = 1.75	4 y 7

Cálculo de frecuencias

Las razones matemáticas de los intervalos permiten calcular la frecuencia de las notas. Partiendo de un la 440 calculamos la frecuencia de do#, mi y sol:

la	do# (tercera mayor desde la)	mi (quinta justa desde la)	sol (séptima menor desde la)
440	440 x 1.25 = 550	440 x 1.5 = 660	440 x 1.75 = 770

Si dividimos por la razón matemática del intervalo obtenemos intervalos descendentes. A continuación calculamos la frecuencia del fa que está una tercera mayor por debajo del la:

Con estos conceptos podemos comenzar a explicar los sistemas de afinación...

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivar 4.0 Internacional.
Publicado por teoria.com.