Harmonic Series

We need to start by explaining a phenomenon known as the harmonic series. When we hear a sound produced by a musical instrument, we are actually hearing a multitude of sounds that constitute the harmonic series.

In the 17th century, the Frenchman Joseph Sauveur (1653-1716) and the Englishman Thomas Pigot (1657-1686) noticed that the strings vibrate in sections, a phenomenon that explains why one string produces this multiplicity of sounds.

The video below shows the spectrum analysis of a C two octaves below middle C (C2). Each peak represents a harmonic of the series:

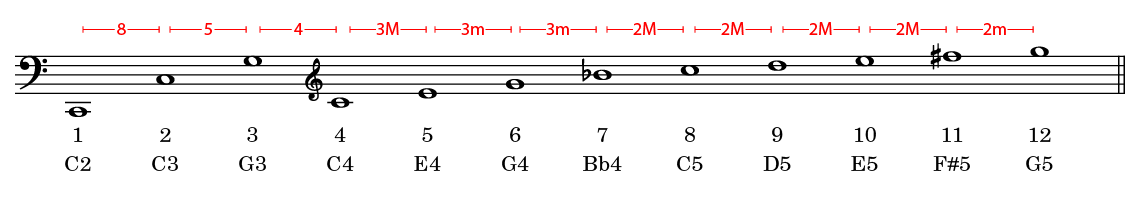
Notes:

• We have written the musical notes corresponding to the first 12 harmonics of the series. Many harmonics follow these first harmonics.
• The first harmonic, or fundamental, is not necessarily the strongest harmonic.
• The balance between the harmonics varies constantly. This, combined with the immense number of harmonics, explains the complexity of synthesizing sounds.

Importance of the harmonic series

The dialogue between human beings and nature, to which we refer in the subtitle of this article, is closely related to the harmonic series. Nature speaks with the harmonic series, and humans answer with tuning systems.

The harmonic series defines many of our intervals. Listed below are the octave, fifth, fourth, major third, and minor seventh:

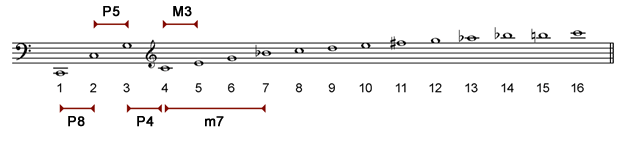
We can calculate the mathematical ratio (or size) by dividing the frequencies of notes. Here we use the frequency of some harmonics to calculate the size of intervals:

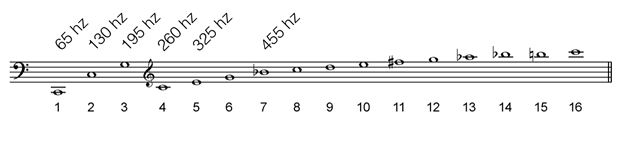
Interval	Ratio	From harmonics
Octave	130 / 65 = 2	1 and 2
Fifth	195 / 130 = 1.5	2 and 3
Fourth	260 / 195 = 1.33	3 and 4
Major third	325 / 260 = 1.25	4 and 5
Minor seventh	455 / 260 = 1.75	4 and 7

It is interesting to note that we can calculate the values using harmonic numbers:

Interval	Ratio	From harmonics
Octave	2 / 1 = 2	1 and 2
Fifth	3 / 2 = 1.5	2 and 3
Fourth	4 / 3 = 1.33	3 and 4
Major third	5 / 4 = 1.25	4 and 5
Minor seventh	7 / 4 = 1.75	4 and 7

Calculating frequencies

The mathematical ratios can be used to calculate the frequency of notes. From an A 440, we calculate the frequency of C#, E and G:

A	C# (major third)	E (perfect fifth)	G (minor seventh)
440	440 x 1.25 = 550	440 x 1.5 = 660	440 x 1.75 = 770

If we divide by the mathematical ratio, we obtain descending intervals. Here we calculate the frequency of an F, a major third below A:

These concepts are essential for the comprehension of the different tuning systems ...

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.