There are more reliable, faster and easier methods to identify and construct intervals than counting whole and half steps. This animation will
let you explore some of them. A brief description of each one:
- Scales - if you know the major and minor scales in your instrument, you can use scales to identify intervals. For example: from D to A, we have a perfect fifth because they are the first and fifth notes of the D major and D minor scales. If the A is sharp, the interval gets bigger and becomes augmented. If the A is flat, the interval gets smaller and becomes diminished.
- Chords - if you know the basic chords in your instrument (or the arpeggios), you can use chords to identify some intervals. For example, we have a perfect fifth from D to A because they are the root and fifth of the D major and D minor chords. If the A is sharp, the interval gets bigger and becomes augmented. If the A is flat, the interval gets smaller and becomes diminished.
- Inversion - This method is handy to work with big intervals like the sixth and the seventh since, after inversion, they become thirds and seconds. Isn't it easier to identify a second than a seventh? See Inversion and Identifying by Using Inversions for
more information.
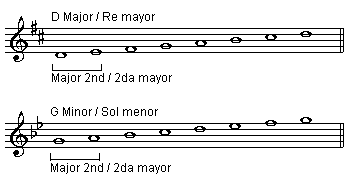
Scales: from the first note to the second note of any major or minor scale, we have a major second.
Chords: from the root of any major chord to its third, we have a major third. In the case of minor chords, the third is minor.

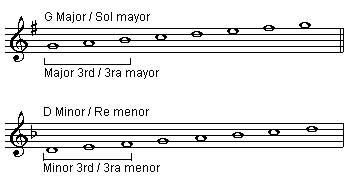
Scales: from the first note to the third note of any major scale, we have a major third. From the first note to the third note of any minor scale, we have a minor third.
Scales: from the first to the fourth note of any major or minor scale, we have a perfect fourth.

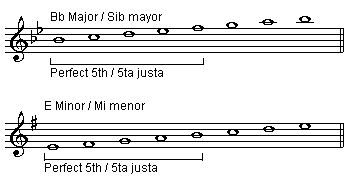
Chords: from the root to the fifth of any major or minor chord, we have a perfect fifth.

Scales: from the first to the fifth note of any major or minor scale, we have a perfect fifth.
Inversion: a sixth inverts into a third. We invert an interval by raising its lower note one octave. Major intervals become minor, minor intervals major, perfect intervals remain perfect, augmented intervals become diminished and diminished intervals become augmented.

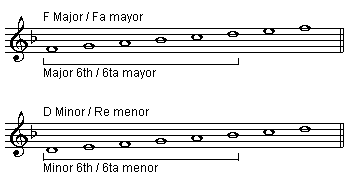
Scales: from the first note to the sixth note of any major scale, we have a major sixth. In minor scales the sixth from the first to the sixth note is minor.
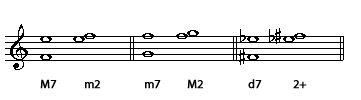
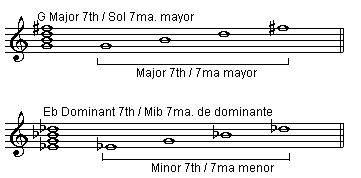
Chords: from the root to the seventh of any major seventh chord, we have a major seventh. From the root to the seventh of any dominant seventh chord, we have a minor seventh.
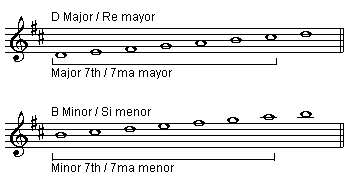
Scales: from the first note to the seventh note of any major scale, we have a major seventh. In minor natural scales, the seventh from the first to the seventh note is minor.
Inversion: a seventh inverts into a second. We invert an interval by raising its lower note one octave. Major intervals become minor, minor intervals major, perfect intervals remain perfect, augmented intervals become diminished and diminished intervals become augmented.