Meantone Temperament

The meantone temperament is described by Francis Salinas in De Musica Libri Septem (1577). In the meantone temperament, major thirds are the same size as those in the harmonic series (1.25) and are divided into two equally sized tones (or mean tones).

The major scale according to the meantone temperament

We are going to build the major scale using the meantone temperament. We start by multiplying the frequency of C by 1.25 (the major third according to the harmonic series):

The major second

Now we find D by dividing the third into two equal steps, how?

The mathematical operation that allows us to find the size is the square root. The square root of the size of the major third gives the size of the major second:

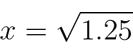
Let's see if it's true:

The square root of 1.25 = 1.118033988749895. This should be the size of the major second:

1. Find D by multiplying C by the size of the major second.
   D = 263 x 1.118033988749895 = 294.04
2. Find E by multiplying D by the size of the major second.
   E = 294.04 x 1.118033988749895 = 328.75

The result is the same as previously calculated, confirming that we have correctly calculated the size of the major second.

The minor second

Now we need to calculate F, a minor second above E. An octave is composed of five major seconds (whole steps) and two minor seconds (half steps). The major seconds: C to D, D to E, E to F#, F# to G# and G# to A#, followed by two minor seconds: A# to B and then B to C.

Mathematically, this is expressed as:

t * t * t * t * t * s * s (t = tone, major second or whole step , s = semitone, minor second or half step)

Or:

t⁵ * s²

This gives us this formula (2 is the octave size):

t⁵ * s² = 2

We know the size of a whole step, so we can write:

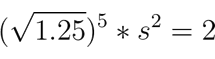
We want to find the value of the minor second. If we divide both sides of the equation by the square root of 1.25 raised to the fifth power, we get

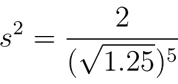
Finally, taking the square root of both sides gives us the size of the minor second:

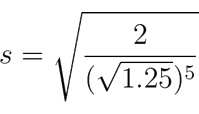
The size of the minor second is then:

s = 1.06998448796228

Finally we find F:

328.75 x 1.06998448796228 = 352.18

Completing the scale

We can now complete the scale. G is a major second above F, so we multiply F by the size of the major second. A is a major third above F and B is a major third above G, so we calculate both notes using the size of the major third:

New problems ...

The mesotonic temperament was effective as long as the number of tonalities in use was limited. When baroque composers began to use less common tonalities the problems became evident. Listening to Bach's Prelude in A-flat major BWV 862 using the mesotonic temperament, we immediately notice the problems:

The meantone fifth is smaller than the acoustic fifth. If we follow a cycle of meantone fifths (C - G - D ... F - C), the last fifth is too large. This fifth is called the wolf fifth.

Listen to the wolf fifth:

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Published by teoria.com.